---

|home|	|software|	|teaching|	|publications|	|photos|
|documents|	|activities|	|research group|	|research|	|about|autor|

---

See Morfometryka page

GALAXY STRUCTURAL ANALYSIS: CLUES FOR THEIR FORMATION AND EVOLUTION

Galaxy morphological properties are a result of their formation, evolution and interaction with their neighborhood. Galaxies in groups or clusters may have diverse evolutionary path compared to those that are isolated, which may reflect in their morphology.

Traditionally, galaxy morphology has been addressed manual and visually: an expert examines images of galaxies and identifies features (or absence of them in the case of ETG) which distinguish the object as belonging to a specific galaxy class (e.g. Hubble 1926, de Vaucouleurs 1959, Sandage 1975, van den Bergh 1976.) This classification paradigm is strongly subjective, it is prune to errors and cannot be applied to the number of galaxies present in SDSS or UKIDS. Thus, it is imperative to quantify the morphology of galaxy as measurable quantities which can be coded in an algorithm.

There has been several attempts to objectively measure galaxy morphology and to classify them accordingly. One relatively successful system is the concentration, asymmetry, smoothness, Gini and M20 (CASGM) system, developed in Abraham (1994), Conselice (2000) and Lotz (2004). The concentration (C) is measured as the fraction of the radius that contain 80% and 20% of the total galaxy light; The asymmetry (A) coefficient compares every two points diametrically opposite relative to the galaxy center; the smoothness (S) measures the small scale structures in the galaxy; the Gini coefficient measures how concentrated is the light among the pixels; the M20 coefficient measure the size of the 20% brighter pixels in the galaxy. These basic set have been enlarged with other measurements: the Sersic model parameters (In,Rn,n) (Sersic 1968); The Petrosian radius (Petrosian 1976); the multi-mode (M), intensity (I) and deviation (D) statistics (Freeman et al 2013), among others.

Such a parametrization of galaxy morphology answer two immediate needs. First, it is possible to duplicate human visual classification by positioning the galaxies in the space of the parameters cited. In such a supervised classification, a set of previously classified galaxies are used to train a discriminant function that will assign to each new galaxy a probability of belonging to each class. Even the simple supervised naïve Bayes algorithm provides robust classification, although more sophisticated schemes such as quadratic discriminant functions or kernel method improve the classification further, at the expense of numerical complexity (Bishop 2006.)

The second reason for establishing a galaxy morphometry system is that we may seek for structures in the parameters space that may give clues for the physical reasons for their formation and evolution that are not visible in the currently human-based mode. The Hubble tuning fork classification does not account for all the details that we can currently measure in galaxy images. Further, it does not hold as we go deep in space even at redshift z=0.25. So, a new classification procedure is needed, both to account for the large amount of data, and also to guide us to find the physics processes that drive galaxy evolution.

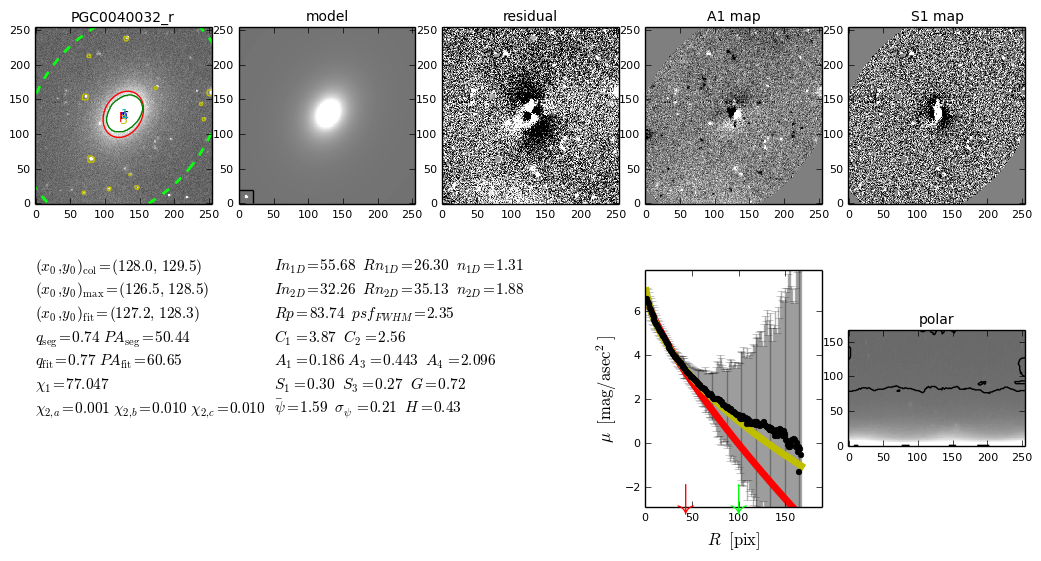
Currently we have implemented an algorithm that operates on galaxy stamp images and measures the morphological parameters automatically. 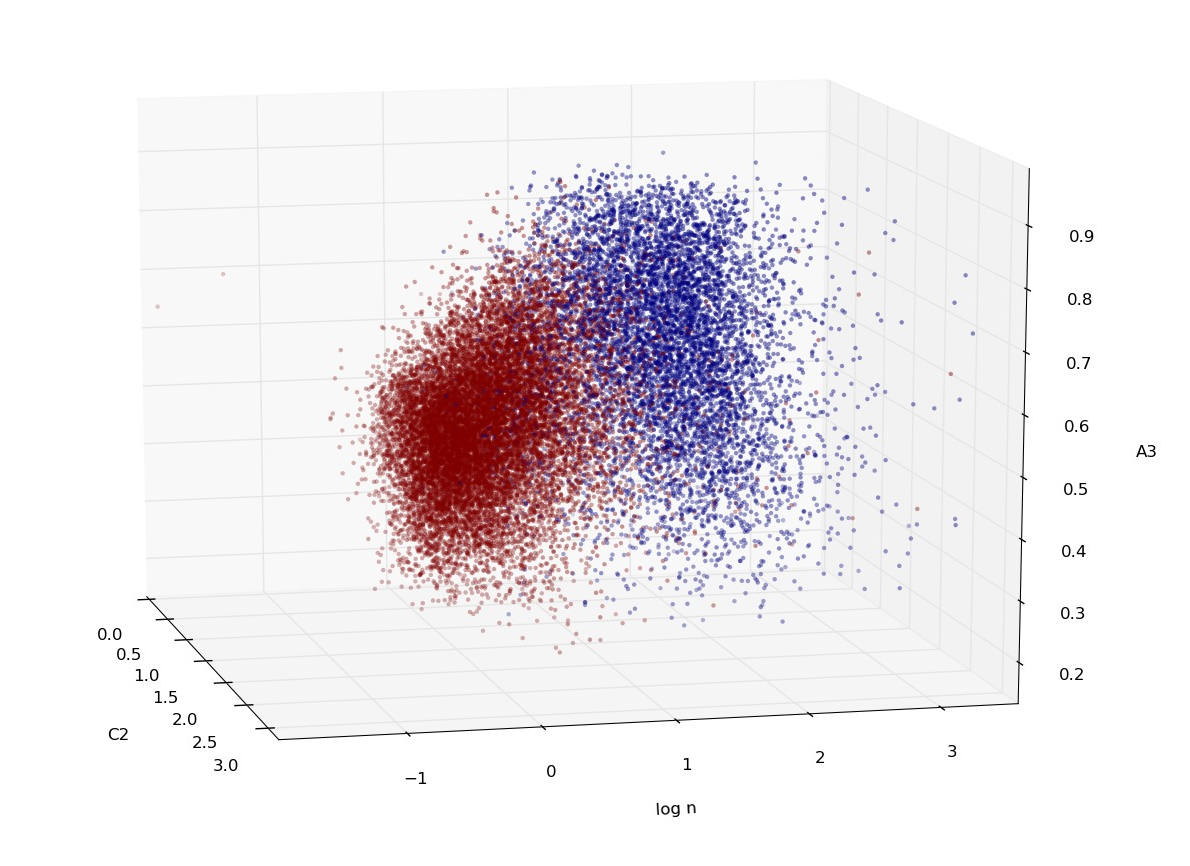The algorithm is called MORFOMETRIKA (Ferrari, 2014.) It takes each galaxy image, subtracts sky background, locates the object, measures the center, axes lengths and position angle; performs aperture photometry and fits a Sersic law to the light profile; measures Petrosian radius, concentration, asymmetry, smoothness and Gini coefficient. MORFOMETRIKA was used to classify 80 000 galaxies training the discriminant function from a set of 20 000 previously classified galaxies. Figure 1 show a subspace of the parameters concentration (C2), asymmetry (A3) and logarithm of Sersic n for the training set; Spiral galaxies are shown in red and elliptical galaxies in blue.